tags interni : nessuno.

Il mondo che ci circonda è a tre dimensioni ma possiamo immaginare e studiare anche la quarta dimensione. Oggi pomeriggio, ne ha parlato Maria Dedò, nella conferenza collegata alla mostra di Leonardo a Bolzano. Sono venuti fuori rapidamente tutti i problemi che nascono dalla nostra mancanza di esperienza della quarta dimensione.
A dire il vero anche immaginare e descrivere un mondo a due dimensioni è una astrazione, perchè triangoli, quadrati e, in generale, le figure geometriche piane non sono oggetto di esperienza.
Nel mondo piatto di Flatlandia, Edwin A. Abbot, racconta di un quadrato che giunge ad immaginare la terza dimensione.
Un sfera, infatti, aveva intercettato il piano bidimensionale e da quel piano poteva essere vista solo come una circonferenza che varia le proprie dimensioni.

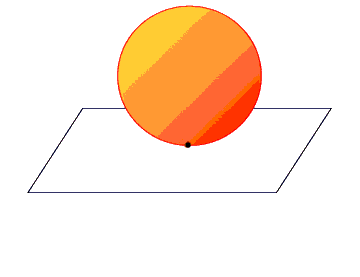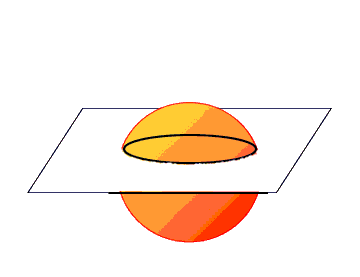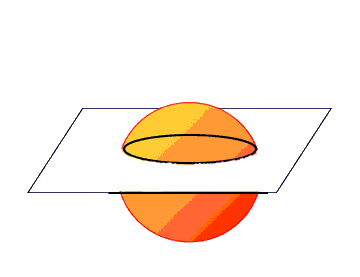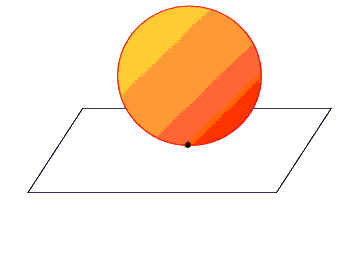
Cosi’ come dal bidimensionale si puo’ immaginare il tridimensionale, dal tridimensionale possiamo immaginare dimensioni superiori, per esempio un mondo di poligoni a quattro dimensioni. In quel mondo il cubo potrebbe essere chiamato ipercubo e si presenterebbe pressappoco così:

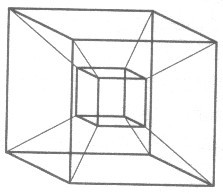
L’immagine è tratta dal libro “Forme- simmetria e topologia” di Maria Dedò.

Ho trovato una bella sintesi di Flatlandia in un lavoro dell’ Istituto tecnico industriale Marconi di Lugo (Ravenna), che merita di essere consultato (cliccare per scaricare il file ppt 1.3 mb).

tags esterni :nessuno.

Questo articolo è stato pubblicato Friday, 11 November 2005 alle 9:36 pm e classificato in Scuola 3d alla mostra di Leonardo. Puoi seguire i commenti a questo articolo tramite il feed RSS 2.0. Puoi inviare un commento, o fare un trackback dal tuo sito.